正方形5つから出来ている十字形をいくつかに切り離し、並べ替えて、同じ面積の正方形を作りなさい。
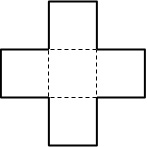
上の問題を初めて見た12歳のころ、ピタゴラスの定理(三平方の定理)を知らかった私は「面積は5で二乗の数ではないのだから、正方形にできないでしょ」としか感じなかったのですが、解説を見て、衝撃を受けました。
ピタゴラスの定理を知らなくても、発想力・想像力次第で正方形ができるところが一番興味深かったのだと思います。
さらに、中学3年生になって三平方の定理を学んだとき、32+42=52 という数式を知って、面積が25の傾いた正方形を作る問題を構想したのです。
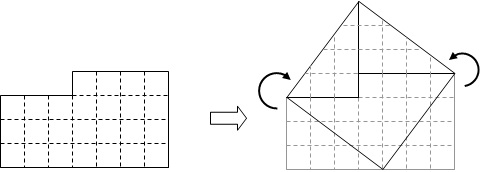
ところが、パズル書籍を読んでいると、このアイデアは既に多々発表されていることが分かり、「既出のアイデアだったら、せっかく出題しても面白くないな」と思ったことがあります。
と同時に、「三平方の定理を使わない、新しい分割法はないか?」という思いが生まれたのですが、すぐに解決することができないまま、時間が流れました。

そして、大学時代。
大学の図書館で勉強もろくにせず、パズルの書籍を読み漁ったり、パズルを作っていたりしていたときのこと。こんな問題を作りました。
問題 左の形(3×9の長方形から一つの角が欠けた形)を3つに切り離し、並べ替えて5×5の正方形を作りたいのですが、どのように切断すればいいでしょう? ただし、並べ替えるときに、ピースは裏返さないでください。
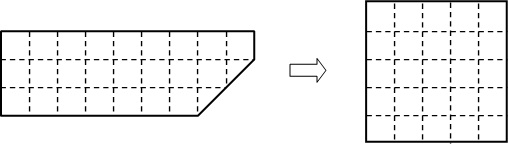
(メディアソフト『ひらめき推理パズルVol.4』にて発表)
面積が25の正方形を作るということは、三平方の定理を使う可能性がある。そういう先入観のあるパズル好きからは、「難しかった」と言われましたが、そのような高等な定理は使わないのです。ほぼ、点線にそって考えていただければいいかと思います。

