ノーマルなナンプレには、3×3のブロックがありますね。
もし、そのブロックを動かせたらどんなパズルになるでしょうか？

ブロックという言い方ではイメージしにくいので、ここからは「フレーム」という言葉に変えて説明します。

例えば、こういう問題。

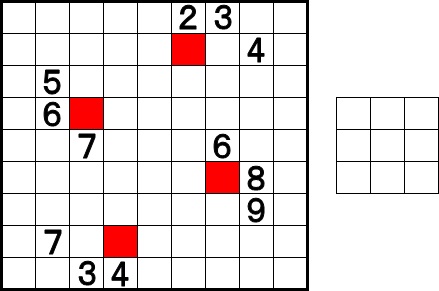
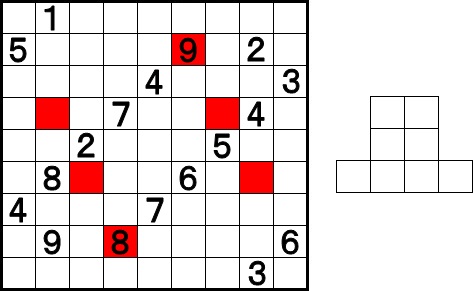
9×9のタテ・ヨコ各列に1～9の数字を一つずつ埋めてください。そのとき、右側のフレーム（ここでは3×3の正方形）をどこに配置しても、その中に1～9の数字が一つずつ入るようにしてください。

ただ、このルールでは問題自体が成立しないので、赤いマスを避けてそのままの向きでフレームを置いたとき、どの場所でもフレーム内に1～9が一つずつ入るように数字を埋めるのです。

ルールが分かりにくいですか？

では、もっと小さい問題で説明します。

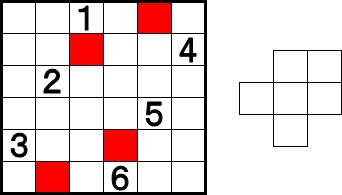
上のような、1～6を一つずつ入れる問題だと……

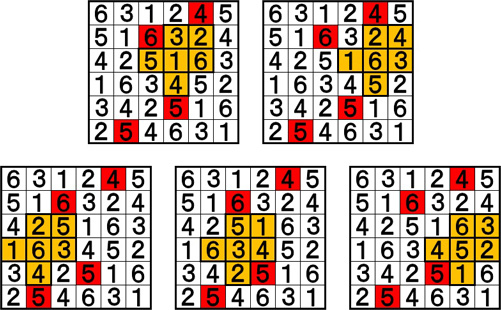
このように、赤マスが入らないよう、そのままの向きでフレームを置きます。そのとき、どこに置いても、フレームの中に1～6の数字が揃うようにする、ということです。

話を9×9に戻します。

さて、このサイズでヒントの数字を一気に最少の8個にまで減らしました。難しめですが、論理的に解けますので、挑戦してみてください。

実は、このようなルールの問題は12年前、「あめしょー」のハンドルネームで「パズルのおもちゃ箱」（現在は閉鎖しています）というサイトに出題したことがあります。

当時、サイズは5×5・6×6・7×7の3種類だけで、今回のような9×9のサイズは作りませんでした。

7×7サイズでも結構難しい問題を出題したので、9×9サイズまで手を出さなくてもいいだろう、という判断だったのですが、その問題を解いたパズルマニアの方から、「全て論理的に解けるのが面白かった」「9×9サイズも解いてみたい」とのご意見をいただいたので、12年の時を経て、9×9バージョンを出題した次第です。

まだまだ問題はありますが、文章が長くなってきたので、最終問題に参ります。

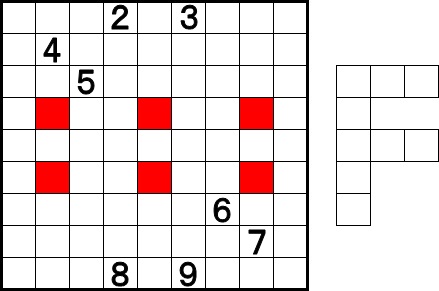
一つ前の問題に比べれば、ヒントの数字は倍以上になっていますが、注目すべきところはフレーム内のマスの個数です。なぜか、8マスしかありません。

どういうことかといいますと、赤いマスを避けて、そのままの向きでフレームを置くとき、どの場所であってもフレーム内に8種類の数字が入るように（同じ数字が存在しないように）、1～9の数字をタテ・ヨコ各列に埋めるのです。

正直、12年前に出題した問題よりもはるかに難しいですが、シラミつぶし法（すべての可能性をチェックしていく方法）を使わず論理的に解けます。

論理パズル好きの方、どうぞご堪能ください。