世のナンプレには、いろんなヒント数字の配置がありますが(以前にも取り上げました)、一番外側のマス(下図の黄色いマス)にしかヒント数字が入っていない問題は作れるでしょうか?

様々なルールを付けると、出来て当たり前になってしまうので、ノーマルなナンプレ(タテ・ヨコ・3×3のブロックにのみ1~9が入るもの)での話です。
もし可能であるなら、ヒントの個数や配置の対称・非対称なんて気にしなくて構いません。ただし、一意解であることは必須の条件です。

例えば、幾何学ナンプレ(タテ・ヨコ・太線で区切られた9マスのブロック内に1~9が一つずつ入るもの)で作ってみました。最初はヒント数字を20個に出来て喜んでいましたが、16個でも論理的に解ける問題が出来ました。

中~上級むけ
でも、いかんせん、9マスのブロックが正方形からかけ離れていて、少々納得いきません。
次は、対角線ナンプレ(ノーマルのナンプレのルールに加え、点線上にある2方向の9マスにも1~9が一つずつ入るもの)で作りました。こちらもヒントが16個で、ロジカルに解ける問題が出来ることは分かりました(これ以上ヒント数を減らした問題には挑戦していません)。
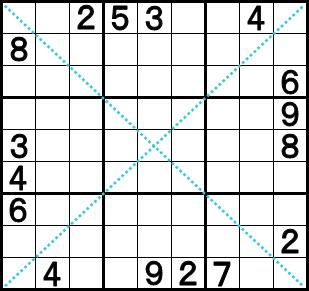
上級むけ
このように、対角線のルールを加えても出来るのですから、ノーマルの問題で出来るかもしれません。
私自身、この問題を可能にする(と思っていた)アイデアをひらめいたのですが、その方法では出来ませんでした。と同時に、不可能なのでは? と思いはじめました。しかし、不可能だという明確な証明はありません。もしかすると、可能なのかもしれません。
最後に、皆さんへ。
もし、この「一番外側のマスにだけヒント数字を入れて作る」ということが可能であれば、1パターンでも見つけてください。不可能であれば、証明をしてください。

